Rappelons que la quantité ![]() , quotient par
, quotient par ![]() du périmètre
du périmètre ![]() de la section, et dite "diamètre moyen périmétrique" (ou, de manière équivalente, "diamètre projectif moyen"), est exactement égale à la moyenne d’un très grand nombre de diamètres mesurés au pied à coulisse dans des directions régulièrement espacées en angle.
de la section, et dite "diamètre moyen périmétrique" (ou, de manière équivalente, "diamètre projectif moyen"), est exactement égale à la moyenne d’un très grand nombre de diamètres mesurés au pied à coulisse dans des directions régulièrement espacées en angle.
Le contour de la section étant représenté en coordonnées polaires par la longueur ![]() du rayon vecteur, le diamètre polaire moyen
du rayon vecteur, le diamètre polaire moyen ![]() correspond à la définition
correspond à la définition
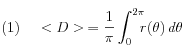
Nous allons, dans ce qui suit, préciser la valeur de la différence ![]() .
.
En coordonnées polaires, le périmètre de la section s’exprime sous la forme :
 , avec
, avec 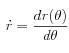 .
.
Divisons (2) par ![]() , il vient :
, il vient :
 .
.
Utilisant le développement
![]() avec
avec![]() , la relation(3) peut être écrite, en utilisant la notation "valeur moyenne"
, la relation(3) peut être écrite, en utilisant la notation "valeur moyenne"  , sous la forme :
, sous la forme :
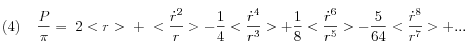 .
.
De sorte que la différence ![]() peut s’écrire, avec
peut s’écrire, avec ![]() :
:
 .
.
La série au second membre de (5) est une série alternée convergeant très rapidement dans les conditions de la pratique courante ( sur les bornes romaines du territoire des Lémovices, les variations relatives de ![]() se limitent à quelques % ). Cette convergence est suffisamment rapide pour que la série puisse être limitée à son premier terme. L’erreur commise dans l’évaluation de
se limitent à quelques % ). Cette convergence est suffisamment rapide pour que la série puisse être limitée à son premier terme. L’erreur commise dans l’évaluation de ![]() ( c’est à dire l’erreur sur la différence) est alors majorée par la valeur absolue du premier terme négligé :
( c’est à dire l’erreur sur la différence) est alors majorée par la valeur absolue du premier terme négligé :  .
.
La différence ![]() entre les diamètres moyens s’écrit donc approximativement :
entre les diamètres moyens s’écrit donc approximativement :

Si le contour de la section est parfaitement circulaire, et à condition de choisir l’origine des coordonnées en son centre,
![]() est une constante et
est une constante et
![]() . Il en résulte, d’après (5), que
. Il en résulte, d’après (5), que ![]() . Les diamètres moyens périmétrique
. Les diamètres moyens périmétrique ![]() et polaire
et polaire ![]() coïncident alors.
coïncident alors.
Avec les non circularités du contour de la section, ![]() et
et ![]() divergent. Nous allons voir que leur écart augmente avec l’amplitude et avec la fréquence angulaire des oscillations du rayon
divergent. Nous allons voir que leur écart augmente avec l’amplitude et avec la fréquence angulaire des oscillations du rayon ![]() autour de sa valeur moyenne.
autour de sa valeur moyenne.
Pour calculer plus facilement ![]() , nous ferons l’approximation supplémentaire
, nous ferons l’approximation supplémentaire
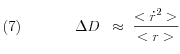
justifiée par le fait que ![]() varie peu (quelques %) et que, de plus,
varie peu (quelques %) et que, de plus, ![]() est nulle lorsque
est nulle lorsque ![]() passe par ses valeurs extrémales. Ce sont donc les valeurs moyennes de
passe par ses valeurs extrémales. Ce sont donc les valeurs moyennes de ![]() qui ont le plus de poids dans la calcul de (6).
qui ont le plus de poids dans la calcul de (6).
Le rayon vecteur ![]() est une fonction périodique de
est une fonction périodique de ![]() , de période
, de période ![]() . Pour calculer (7), il est commode de développer
. Pour calculer (7), il est commode de développer ![]() en série de FOURIER, c’est à dire en une somme de fonctions sinusoïdales de fréquences
en série de FOURIER, c’est à dire en une somme de fonctions sinusoïdales de fréquences ![]() et ses multiples :
et ses multiples :
 .
.
Comme ![]() pour
pour ![]() , on voit que la constante
, on voit que la constante ![]() n’est autre que la valeur moyenne
n’est autre que la valeur moyenne ![]() de
de ![]() . Les deux autres quantités au second membre de (8) représentent donc le défaut de circularité du contour. Le contour est un cercle parfait, de rayon
. Les deux autres quantités au second membre de (8) représentent donc le défaut de circularité du contour. Le contour est un cercle parfait, de rayon ![]() , lorsque les amplitudes
, lorsque les amplitudes ![]() des composantes sinusoïdales du défaut de circularité sont nulles pour
des composantes sinusoïdales du défaut de circularité sont nulles pour ![]() .
.
La dérivée ![]() de
de ![]() s’écrit :
s’écrit :
 .
.
On vérifie facilement que ![]() et que
et que ![]() lorsque
lorsque ![]() et
et ![]() sont différents.
sont différents.
Revenant à (7), il en résulte que :
 .
.
Il est donc possible de passer du diamètre polaire moyen ![]() au diamètre moyen périmétrique
au diamètre moyen périmétrique ![]() par une correction additive :
par une correction additive :
 .
.
La correction ![]() est faible si les défauts de circularité restent "raisonnables". Expérimentalement, sur les vingt bornes romaines maintenant connues en territoire lémovice,
est faible si les défauts de circularité restent "raisonnables". Expérimentalement, sur les vingt bornes romaines maintenant connues en territoire lémovice, ![]() va de de 2 à 5 mm pour des diamètres moyens
va de de 2 à 5 mm pour des diamètres moyens ![]() de l’ordre de 55 cm.
de l’ordre de 55 cm.
Le diamètre polaire moyen ![]() , qui vaut
, qui vaut ![]() , ainsi que les amplitudes
, ainsi que les amplitudes ![]() des composantes sinusoïdales du défaut de circularité, sont calculables (de manière approchée) au moyen de la transformation de Fourier discrète (TFD), à partir des échantillons du contour de la section relevés au cercle gradué. Le côté approximatif de ce calcul provient du fait que le contour de la section n’est connu qu’en un nombre fini N de points d’échantillonnage. Naturellement, la précision des résultats augmente avec N. Concernant les bornes romaines en Limousin, les mesures sur le terrain nous ont montré que la valeur N = 32 (
des composantes sinusoïdales du défaut de circularité, sont calculables (de manière approchée) au moyen de la transformation de Fourier discrète (TFD), à partir des échantillons du contour de la section relevés au cercle gradué. Le côté approximatif de ce calcul provient du fait que le contour de la section n’est connu qu’en un nombre fini N de points d’échantillonnage. Naturellement, la précision des résultats augmente avec N. Concernant les bornes romaines en Limousin, les mesures sur le terrain nous ont montré que la valeur N = 32 (![]() ) est tout à fait suffisante pour obtenir la précision millimétrique nécessaire à la détermination des amplitudes
) est tout à fait suffisante pour obtenir la précision millimétrique nécessaire à la détermination des amplitudes ![]() et
et ![]() . Le choix d’une puissance de 2 pour N est lié aux possibilités d’utilisation d’algorithmes courants de transformée de Fourier rapide pour ce calcul de TFD.
. Le choix d’une puissance de 2 pour N est lié aux possibilités d’utilisation d’algorithmes courants de transformée de Fourier rapide pour ce calcul de TFD.
( à suivre )
Dernière mise à jour : 30 octobre 2012.
 bornimétrie
bornimétrie